1.3 Model Selection
One of the commonly used technique for model selection is cross-validation. In a $S-fold$ cross-validation, training set is divided into $S$ equal subests where one of the subset is used for model vaidation and the remaining $S-1$ sets will be used for model training. This means that a total fraction of $\frac{S-1}{S}$ of dataset is used for model training. For a scarce dataset, it is common practice to set $S=N$, which is called as leave-one-out cross-validation technique. One of the major drawback of cross-validation is that we need to run $S$ training runs for $S$ subsets. The ideal model validation technique should rely only on training data and allow the comparison of multiple hyperparameters and model types in a single training run.
1.4 Curse of Dimensionality
One rudimentary way to design a classification or rgression algorithm is to divide the whole region containing the data points into small cells and take decision based on the distribution of training points in the individual cells. For example, in a calssification problem, we can find the cell to which a new point which has to be classified belongs, and assign it the highest occuring class of that cell. A simple $2D$ representation is shown in the middle figure below.
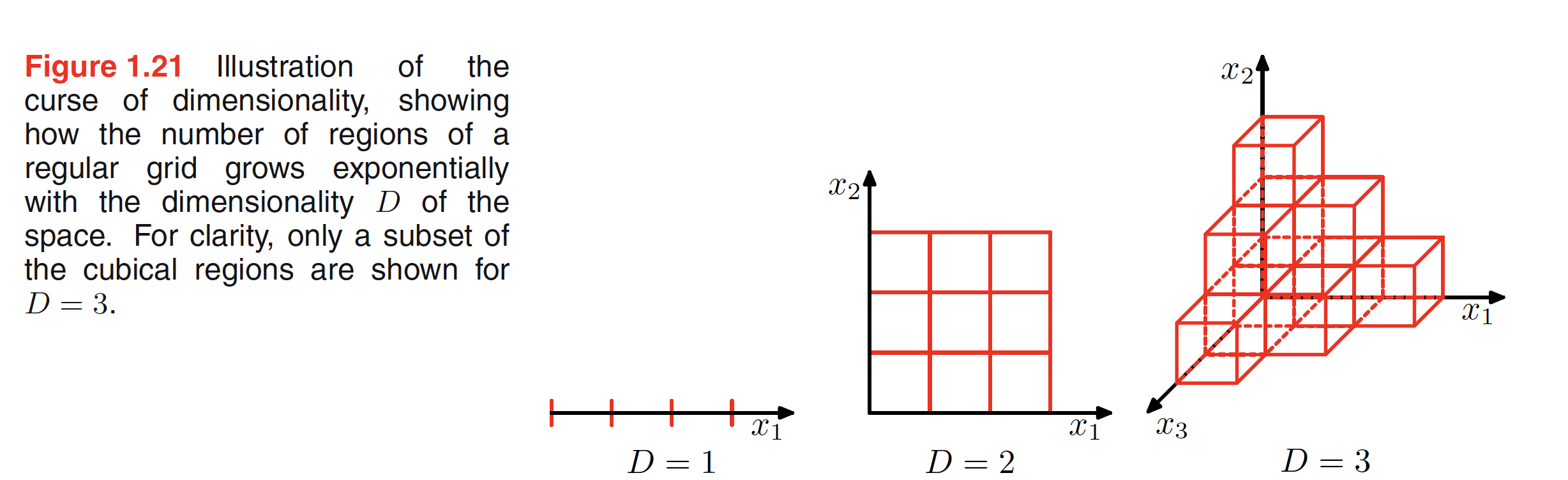
As we see in the above figure, if the dimension keeps on inreasing, the number of cells will increase exponentially given the interval is kept constant across all dimensions. To ensure that the cells are not empty, we will need exponentially large number of training data. One of the major reason for not understanding the problem related to higher dimension is our limitation in visualizing any space higher than $3D$. As an example, for a $D$ dimensional sapce, the fraction of the volume of sphere that lies between radis $r=1-\epsilon$ and $r=1$ can be given as $\frac{V_D(1) - V_D(1 - \epsilon)}{V_D(1)}$, where $V_D(r) = K_Dr^D$. This gives the fraction as $\frac{V_D(1) - V_D(1 - \epsilon)}{V_D(1)} = 1 - (1 - \epsilon)^D$. For large $D$, even for small value of $\epsilon$, this fraction will be close to $1$, for example, for a $30$ dimensional spce, $96%$ of it’s volume will be concentrated in the last $10%$ (outer most shell) of the sphere. This means that not all the intutions developed in spaces of low dimensionality will work well in a higher dimension space. Hence, to make the lower dimension pattern recognition techniques to work in high dimension settings, certain transformations to the dataset are needed.