8.1 Four Fundamental Subspaces
The four fundamental subspaces for a $m \times n$ matrix $A$ are as follows:
- Column Space $C(A)$ in $\mathbb{R}^m$
- Null Space $N(A)$ in $\mathbb{R}^n$: Solution to $Ax=0$
- Row Space $C(A^T)$ in $\mathbb{R}^n$: All combinations of the rows of $A$ or we can say that all combinations of the columns of $A^T$
- Left Null Space of $A^T$ $N(A^T)$ in $\mathbb{R}^m$: Solution to $A^Ty=0$ and is also called as Left Null Spcae of $A$
The pictorial representation of these spaces with their dimension and basis is as follows:
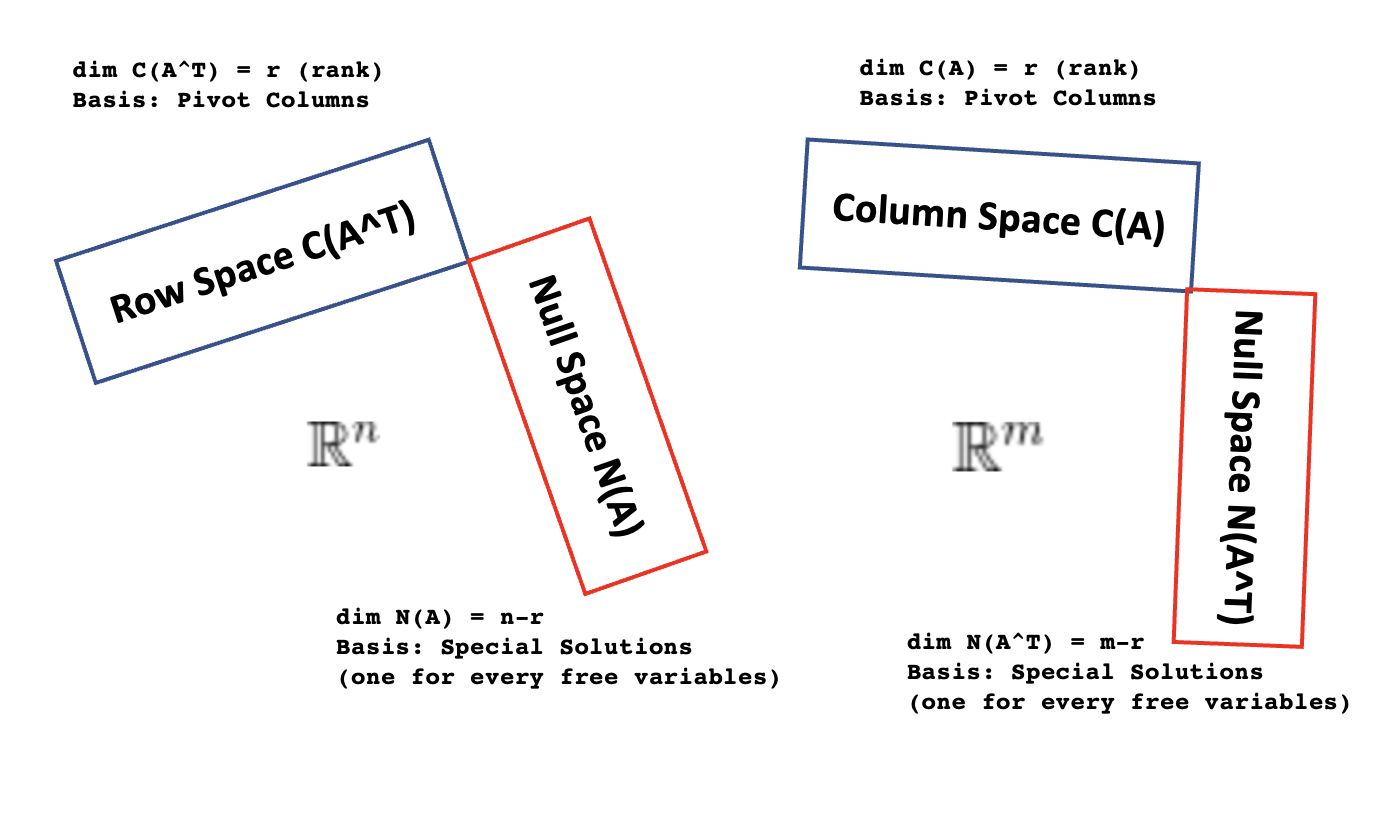
Let’s take an example matrix $A$ to understand these four subspaces in a better way.
$$\begin{align} A = \begin{bmatrix} 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 1 \\ 1 & 2 & 3 & 1 \end{bmatrix} \xrightarrow{\text{S1}} \begin{bmatrix} 1 & 2 & 3 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \xrightarrow{\text{S2}} \begin{bmatrix} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} = R \end{align}$$
where, the performed row operations on the matrix $A$ are: $S1: row_2 = -1(row_2 - row_1);row_3 = row_3 - row_1$ and $S2:row_1 = (row_1 - 2 \times row_2)$. The resultant matrix $R$ can be represented as:
$$\begin{align} R = \begin{bmatrix} I & F \\ 0 & 0 \end{bmatrix}; I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} F = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix} \end{align}$$
8.1.1 Column Space & Null Space
Column Space $C(A)$ is formed by the pivot columns of the reduced-row echelon matrix $R$. It’s dimension is $r$ where $r$ is the rank of the matrix or number of pivot columns in it. One important thing to note is: Row operations DO NOT preserve the Column Space. (as the column space of $A$ and $R$ are different). i.e. $C(A) \neq C(R)$.
Null Space is the solution of the equation $Ax=0$. As discussed in the previous post, the dimension of null space is the number of free variables which is $n-r$.
8.1.2 Row Space
The matrix $R$ is obtained by row operations on $A$. Row operations preserve the Row Space. The basis for the row space of matrix $A$ is the first $r$ rows of $R$. The logic of first $r$ columns is not true for $A$ as row exchange can be one of the steps in the row operations. The reason for row operation preserving the row space is the fact that it only consists of linear operations on each of the row. Every row operation transforms the row linearlly by taking linear combinations of different rows in the matrix. As all linear combinations of the vectors in a subspace lie in the subspace itself, row operations do not preserve the row space. The dimension of row space is $r$ as there will be $r$ pivots and hence $r$ non-zero rows in $R$.
8.1.3 Left Null Space
Left Null Space, also called as null-space of $A^T N(A^T)$ is the vector spcae spanned by the solution of the equation $A^Ty=0$. The row reduction steps which transform $A$ to $R$ can be encoded in a matrix $E$ such that $EA=R$. $E$ can be obtained by performing the same steps on an Identity Matrix.
$$\begin{align} I = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \xrightarrow{\text{S1}} \begin{bmatrix} 1 & 0 & 0 \\ 1 & -1 & 0 \\ -1 & 0 & 1 \end{bmatrix} \xrightarrow{\text{S2}} \begin{bmatrix} -1 & 2 & 0 \\ 1 & -1 & 0 \\ -1 & 0 & 1 \end{bmatrix} = E \end{align}$$
Hence, the above row reduction procedure can be written as:
$$\begin{align} \begin{bmatrix} -1 & 2 & 0 \\ 1 & -1 & 0 \\ -1 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 1 \\ 1 & 2 & 3 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \end{align}$$
Now, finding Left Null Space means finding the solution of $A^Ty=0$. This means, we have to find the combinations of rows of $A$ (or columns of $A^T$) which gives us the $0$ vector. If we look at the above equation, the last row of $R$ is a zero vector which we get by multiplying the matrix $A$ by $\begin{bmatrix}-1 & 0 & 1\end{bmatrix}$.
$$\begin{align} \begin{bmatrix} -1 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 1 \\ 1 & 2 & 3 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 0 & 0 & 0 \end{bmatrix} \end{align}$$
Hence, we can say that the basis of Left Null Space is formed by the rows in E corresponding to the zero vector in $R$. It’s dimension will be $m-r$ as there will be $m-r$ (number of rows - pivot rows) zero vector rows in $R$.