1.1 The Geometry of Linear Equations
The fundamental goal of linear algebra is to solve a system of linear equations. Let us look at an example of a set of $2$ linear equations in $2$ unknowns:
$$\begin{align} 2x-y = 0 \\ -x+2y = 3 \end{align}$$
The above system of linear equation when written in matrix multiplication form can be represented as $Ax = b$ where $A$ is a $2 \times 2$ matrix, $x$ and $b$ are column vectors.
$$\begin{align} \begin{bmatrix} 2 & -1 \\ -1 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} \end{align}$$
There are two ways to geometrically interpret the above system of linear equations. The first one can is called as: row picture of the system of linear equations. In this, we plot each of the individual equations and try to find the common intersection point (if exist) of all of them. The point of intersection is the solution to the system of equations. For the above system, the geometrical interpretation based on the row picture is shown below giving $(1,2)$ as solution.
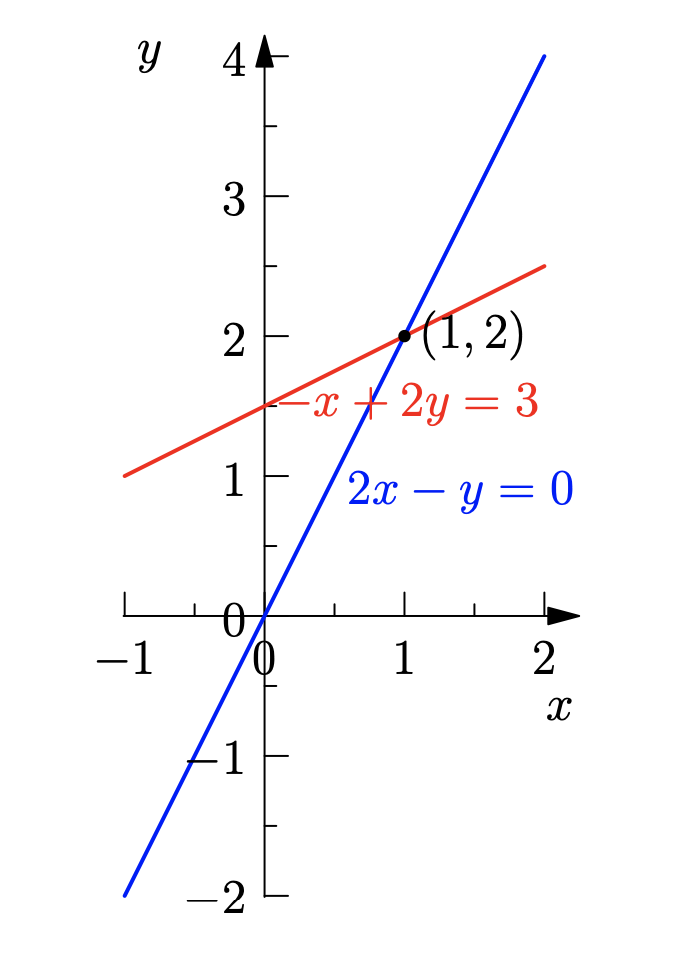
The above system of linear equation can be rewritten as
$$\begin{align} x\begin{bmatrix} 2 \\ -1 \end{bmatrix} +y\begin{bmatrix} -1 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ 3 \end{bmatrix} \end{align}$$
which is the linear combination of the column vectors. The above mentioned way of representing the system of linear equations is called as column picture and can be geometrically interpreted as shown in the below figure. It should be noted that the solution of the equation is $(1,2)$ as $\begin{bmatrix} 2 \ -1 \end{bmatrix}$ when combined with twice of $\begin{bmatrix} -1 \ 2 \end{bmatrix}$ gives $\begin{bmatrix} 0 \ 3 \end{bmatrix}$.
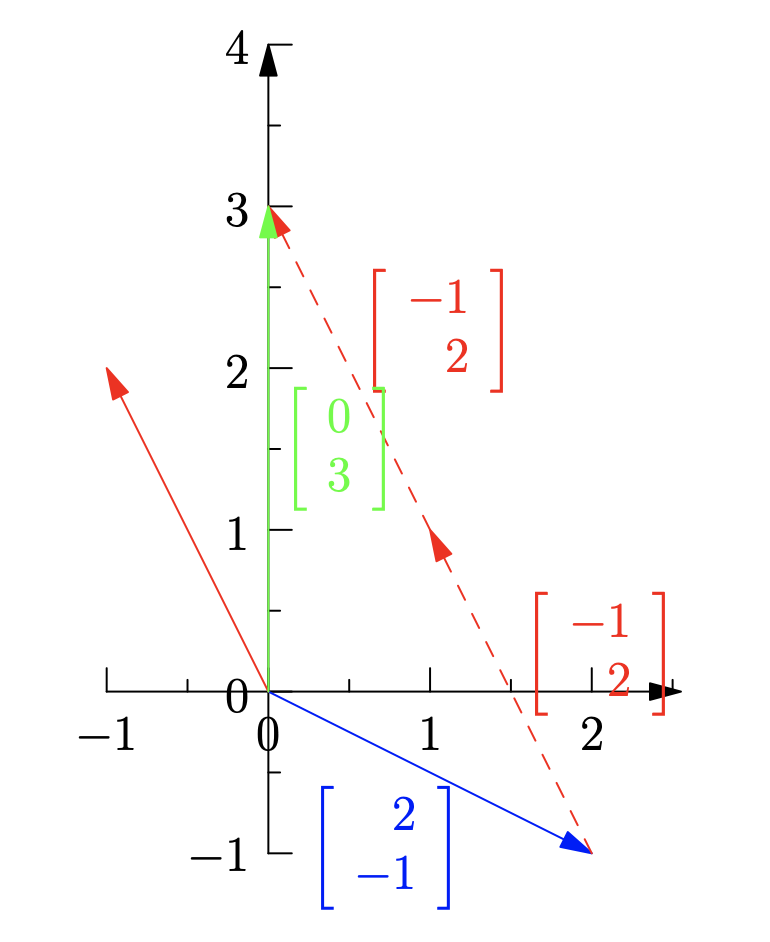
1.2 Matrix Multiplication
Matrix Multiplication can be interpreted and done in different ways. All the discussed methods have different geometrical significance. Let $A,B$ and $C$ are $m \times n$, $n \times p$ and $m \times p$ matrices respectively such that $AB=C$ and $a_{ij}, b_{ij}, c_{ij}$ be the individual elements in row $i$ and column $j$ of the respective matrices.
For the demonstration purpose, let the matrices $A,B$ be
$$\begin{align} A = \begin{bmatrix} 2 & -1 & 3\\ -1 & 2 & 4 \end{bmatrix}, B = \begin{bmatrix} 0 & 1\\ 2 & 1 \\ 3 & 5 \end{bmatrix} \end{align}$$
- Standard Method (Row times Column): The entry in cell $(i,j)$ of the resultant matrix $C$ is the dot product of $i^{th}$ row of first matrix $A$ and $j^{th}$ column of second matrix $B$.
$$\begin{align} C_{11} = \begin{bmatrix} 2 & -1 & 3 \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 2 \\ 3 \end{bmatrix} = 7 \end{align}$$
$$\begin{align} C_{12} = \begin{bmatrix} 2 & -1 & 3 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 1 \\ 5 \end{bmatrix} = 16 \end{align}$$
$$\begin{align} C_{21} = \begin{bmatrix} -1 & 2 & 4 \end{bmatrix} \cdot \begin{bmatrix} 0 \\ 2 \\ 3 \end{bmatrix} = 16 \end{align}$$
$$\begin{align} C_{22} = \begin{bmatrix} -1 & 2 & 4 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 1 \\ 5 \end{bmatrix} = 21 \end{align}$$
$$\begin{align} C = \begin{bmatrix} C_{11} & C_{12} \\ C_{21} & C_{22} \end{bmatrix} = \begin{bmatrix} 7 & 16 \\ 16 & 21 \end{bmatrix} \end{align}$$
- Columns: The entry in the column $j$ of the resultant matrix $C$ is the product of first matrix $A$ and column $j$ of the second matrix $B$. This means that columns of $C$ are combinations of columns of $A$.
$$\begin{align} C_{_1} = \begin{bmatrix} 2 & -1 & 3 \\ -1 & 2 & 4 \end{bmatrix} \begin{bmatrix} 0 \\ 2 \\ 3 \end{bmatrix} = 0\begin{bmatrix} 2 \\ -1 \end{bmatrix} +2\begin{bmatrix} -1 \\ 2 \end{bmatrix} +3\begin{bmatrix} 3 \\ 4 \end{bmatrix} =\begin{bmatrix} 7 \\ 16 \end{bmatrix} \end{align}$$
$$\begin{align} C_{_2} = \begin{bmatrix} 2 & -1 & 3 \\ -1 & 2 & 4 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 5 \end{bmatrix} = 1\begin{bmatrix} 2 \\ -1 \end{bmatrix} +1\begin{bmatrix} -1 \\ 2 \end{bmatrix} +5\begin{bmatrix} 3 \\ 4 \end{bmatrix} =\begin{bmatrix} 16 \\ 21 \end{bmatrix} \end{align}$$
$$\begin{align} C = \begin{bmatrix} C_{_1} & C_{_2} \end{bmatrix} = \begin{bmatrix} 7 & 16 \\ 16 & 21 \end{bmatrix} \end{align}$$
- Rows: The entry in $i^{th}$ row of matrix $C$ is the product of $i^{th}$ row of matrix $A$ and matrix $B$. This means that rows of $C$ are combination of rows of $B$. $$\begin{align} C_1 = \begin{bmatrix} 2 & -1 & 3 \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 2 & 1 \\ 3 & 5 \end{bmatrix} = 2\begin{bmatrix} 0 & 1 \end{bmatrix} + -1 \begin{bmatrix} 2 & 1 \end{bmatrix} +3\begin{bmatrix} 3 & 5 \end{bmatrix} =\begin{bmatrix} 7 & 16 \end{bmatrix} \end{align}$$
$$\begin{align} C_2 = \begin{bmatrix} -1 & 2 & 4 \end{bmatrix} \begin{bmatrix} 0 & 1\\ 2 & 1\\ 3 & 5 \end{bmatrix} = -1\begin{bmatrix} 0 & 1 \end{bmatrix} +2\begin{bmatrix} 2 & 1 \end{bmatrix} +4\begin{bmatrix} 3 & 5 \end{bmatrix} =\begin{bmatrix} 16 & 21 \end{bmatrix} \end{align}$$
$$\begin{align} C = \begin{bmatrix} C_1 \\ C_2 \end{bmatrix} = \begin{bmatrix} 7 & 16 \\ 16 & 21 \end{bmatrix} \end{align}$$
- Columns time Rows: Another way to multiply matrices is by taking the columns in the first matrix $A$ and multiply it by the corresponding rows in the second matrix $B$ and sum all the resultant matrices together.
$$\begin{align} C_{1} = \begin{bmatrix} 2\\ -1 \end{bmatrix} \begin{bmatrix} 0 & 1 \end{bmatrix} = \begin{bmatrix} 0 & 2 \\ 0 & -1 \end{bmatrix} \end{align}$$
$$\begin{align} C_{2} = \begin{bmatrix} -1\\ 2 \end{bmatrix} \begin{bmatrix} 2 & 1 \end{bmatrix} = \begin{bmatrix} -2 & -1 \\ 4 & 2 \end{bmatrix} \end{align}$$
$$\begin{align} C_{3} = \begin{bmatrix} 3\\ 4 \end{bmatrix} \begin{bmatrix} 3 & 5 \end{bmatrix} = \begin{bmatrix} 9 & 15 \\ 12 & 20 \end{bmatrix} \end{align}$$
$$\begin{align} C = C_{1} + C_{2} + C_{3} = \begin{bmatrix} 0 & 2 \\ 0 & -1 \end{bmatrix} + \begin{bmatrix} -2 & -1 \\ 4 & 2 \end{bmatrix} + \begin{bmatrix} 9 & 15 \\ 12 & 20 \end{bmatrix} = \begin{bmatrix} 7 & 16 \\ 16 & 21 \end{bmatrix} \end{align}$$
- Block Multiplication: Matrices can be multiplied by dividing the matrices into conforming blocks and then multiplying those blocks together. For example, matrices $A$ and $B$ can be divided into confirming blocks as follows.
$$\begin{align} A = \left[\begin{array}{c c| c} 2 & -1 & 3\\ -1 & 2 & 4 \end{array}\right]; B = \left[\begin{array}{c c} 0 & 1 \\ 2 & 1 \\ \hline 3 & 5 \end{array}\right] \implies A = \left[\begin{array}{c | c} A_{22} & A_{21} \end{array}\right]; B = \left[\begin{array}{c c} B_{22} \\ \hline B_{12} \end{array}\right] \end{align}$$
where $$\begin{align} A_{22} = \left[\begin{array}{c c} 2 & -1\\ -1 & 2 \end{array}\right]; A_{21} = \left[\begin{array}{c} 3\\ 4 \end{array}\right]; B_{22} = \left[\begin{array}{c c} 0 & 1\\ 2 & 1 \end{array}\right]; B_{12} = \left[\begin{array}{c c} 3 & 5 \end{array}\right] \end{align}$$
$$\begin{align} AB = \left[\begin{array}{c | c} A_{22} & A_{21} \end{array}\right] \left[\begin{array}{c c} B_{22} \\ \hline B_{12} \end{array}\right] = A_{22}B_{22} + A_{21}B_{12} = \left[\begin{array}{c c} 2 & -1\\ -1 & 2 \end{array}\right] \left[\begin{array}{c c} 0 & 1\\ 2 & 1 \end{array}\right] + \left[\begin{array}{c} 3\\ 4 \end{array}\right] \left[\begin{array}{c c} 3 & 5 \end{array}\right]\end{align}$$
$$\begin{align}
= \left[\begin{array}{c c}
-2 & 1\\
4 & 1
\end{array}\right] + \left[\begin{array}{c c}
9 & 15\\
12 & 20
\end{array}\right]
= \left[\begin{array}{c c}
7 & 16\\
16 & 21
\end{array}\right]
\end{align}$$