14.1 Orthonormal Vectors & Orthogonal Matrices
A set of Orthonormal Vectors can be defined as:
$$\begin{align} q_i^Tq_j = \begin{cases} 0 ,& \text{if } i \neq j \\ 1 ,& \text{if } i=j \end{cases} \end{align}$$
When these set of $n$ orthonormal vectors are put into a matrix $Q$ such that $Q = \begin{bmatrix} q_1 & q_2 & … & q_n \end{bmatrix}$, then we get $Q^TQ = I$. It should be noted that $Q$ doesn’t have to be a square matrix. When $Q$ is a square matrix, we can call it Orthogonal. If $Q$ is a square matrix, $Q^TQ=I$ gives us $Q^T=Q^{-1}$. Hence, a square matrix whose columns are $\perp$ to each other and are of unit length is called as orthogonal matrix. One of the example of orthogonal matrix is given below.
$$\begin{align} Q = \frac{1}{2}\begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \end{bmatrix} \end{align}$$
A rectangular matrix with orthonormal columns is shown below.
$$\begin{align} Q = \frac{1}{3}\begin{bmatrix} 1 & -2 & 2 \\ 2 & -1 & -2 \\ 2 & 2 & 1 \end{bmatrix} \end{align}$$
One of the most important property of a rectangular matrix with orthonormal columns is the ease in the computation of projection matrix $P$. Projection matrix for any matrix $Q$ is given as $P=Q(Q^TQ)^{-1}Q^T$. As $Q$ has orthonormal columns, $Q^TQ = I$ and hence $P=Q(Q^TQ)^{-1}Q^T = QIQ^T = QQ^T$. For an orthogonal matrix $Q$ (square matrix with orthonormal columns), the projection matrix $P=I$.
Now for the solution of the equation $Ax=b$. If $A=Q$, the equation reduces to $Qx=b \implies Q^TQx=Q^Tb \implies x=Q^Tb$. This makes solving the equation less compue intensive as inverse of the matrix is not involved. Each individual components of $x$ can be given as $x_i = q_i^Tb$. Or we can say that the projection on the $i^{th}$ basis vector is just $q_i^Tb$.
14.2 Gram-Schmidt Method
The main goal of Gram-Schmidt Method is to convert any set of vectors into orthonormal vectors. Let $a,b$ be two vectors. We have to convert them into orthonormal set of vectors. The conversion steps are as follows, where $A,B$ are orthogonal vectors obtained from $a,b$ and $q_A,q_B$ are the final orthonormal vectors:
$$\begin{align} a,b \rightarrow A,B \rightarrow q_A = \frac{A}{\lVert A \rVert}, q_B = \frac{B}{\lVert B \rVert} \end{align}$$
We can take $A=a$. If we revisit the way we take projection of $b$ onto $a$, the error $e$ is $\perp$ to $a$ and hence can be taken as $B$. i.e. $B = e = b - \frac{A^Tb}{A^TA}A$. To confirm whether $A \perp B$, we should have $A^TB=0$. $A^TB = A^T(b - \frac{A^Tb}{A^TA}A) = 0$.
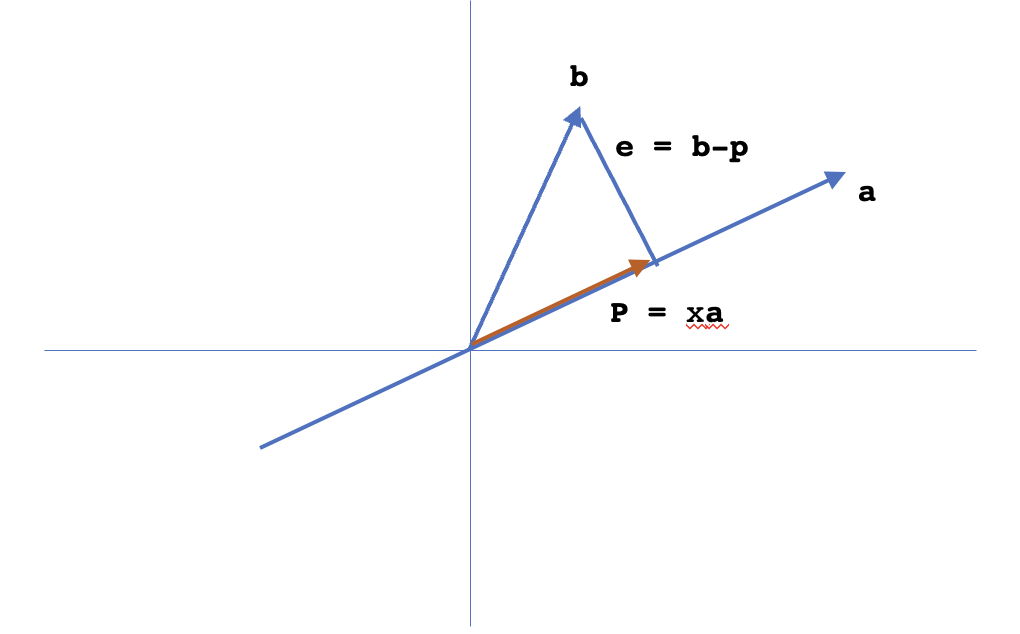
Similarly, for a set of three vectors $a,b,c$ the transformation steps are:
$$\begin{align} a,b,c \rightarrow A,B,C \rightarrow q_A = \frac{A}{\lVert A \rVert}, q_B = \frac{B}{\lVert B \rVert}, q_C = \frac{C}{\lVert C \rVert} \end{align}$$
We can compute $A,B$ and hence $q_A,q_B$ the same way as we did for a two vector case. To get $C$, we have to remove the projections of $c$ along the direction of $A$ and $B$ from it. Hence, $C = c - \frac{A^Tc}{A^TA}A - \frac{B^Tc}{B^TB}B$.
Example:
$$\begin{align} a = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}, b = \begin{bmatrix} 1 \\ 0 \\ 2 \end{bmatrix} \implies A = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}, B = \begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix} - \frac{3}{3}\begin{bmatrix} 1 \\ 0 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ -1 \\ 1 \end{bmatrix} \end{align}$$
$$\begin{align} q_A = \frac{1}{\sqrt{3}}\begin{bmatrix} 1 \\ 1 \\ 1 \end{bmatrix}, B = \frac{1}{\sqrt{2}}\begin{bmatrix} 0 \\ -1 \\ 1 \end{bmatrix} \end{align}$$
Finally, a matrix $A$ whose columns are $a,b$ and is denoted as $A = \begin{bmatrix} a & b \end{bmatrix}$ can be decomposed as $A=QR$ where $Q = \begin{bmatrix} q_A & q_B \end{bmatrix}$ and $R$ is upper triangular. $R$ is upper triangular beacuse later columns of $Q$ are all perpendicular to the former ones.