12.1 Projections in one-dimensional Space
Given two vectors $a,b$ in a plane, the projection of $b$ onto $a$ is shown below. The projection $p$ will be a multiple of $a$ and the error vector $e$ will be orthogonal to $a$. Error vector can be denoted as: $e = b - p$. As $e \perp a$, we can say that: $a^Te =0 \implies a^T(b - p) = 0 \implies a^T(b - xa) = 0 \implies xa^Ta = a^Tb \implies x = \frac{a^Tb}{a^Ta}$. Hence, $p = ax = a\frac{a^Tb}{a^Ta}$.
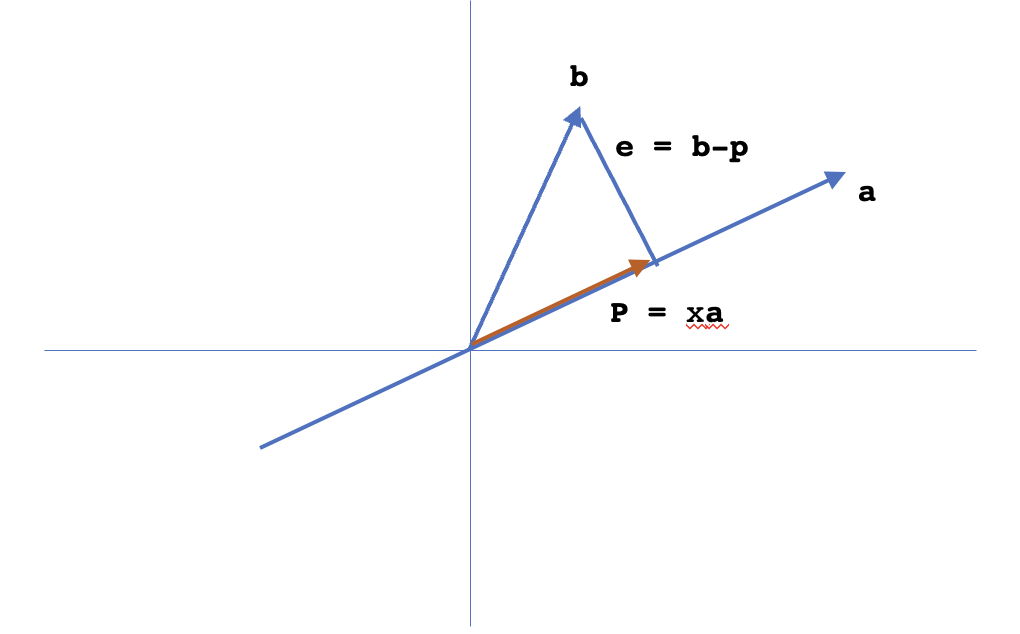
Some of the observations about the projection $p$ are as follows:
- If $b$ is doubled, projection $p$ is doubled
- Change in magnitude of $a$ doesn’t affect projection $p$
- Projection $p$ can be obtained by multiplying $b$ by a projection matrix $P$, where $P = \frac{aa^T}{a^Ta}$. For a vector $a$, $a^Ta$ is a number and $aa^T$ is a matrix.
- Column Space of $P, C(P)$ is the line through $a$
- $Rank(P) = 1$
- Projection Matrix $P$ is symmetric as $P^T = (\frac{aa^T}{a^Ta})^T = \frac{(aa^T)^T}{a^Ta} = \frac{aa^T}{a^Ta} = P$
- For projection matrix $P$, $P^2 = P$ as taking the projection of the projection will land us on the same vector $p$.
12.1.1 Why take Projections?
For any $m \times n$ matrix $A$ such that $m > n$, our goal is to solve $Ax=b$ when it has no solution. The reason for $Ax=b$ to have no solution is the fact that $Ax$ will always be in the column space of $A$ but $b$ may not. In these cases, we can project $b$ on the column space of $A$ and solve for $Ax=p$ instead where $p$ is the projection of $b$ on $C(A)$.
12.2 Projections in multi-dimensional Space
Let $A$ be a matrix representing a two-dimensional space with the basis as vectors $a_1$ and $a_2$, i.e. $A = \begin{bmatrix}a_1 & a_2 \end{bmatrix}$. Let $b$ be the vector whose projection needs to be taken on $A$. The projection $p$ will be in the plane and can be denoted as $p=a_1\hat{x_1} + a_2\hat{x_2}$ or $p=A\hat{x}$. The error $e$, which is $e = b-p = b-A\hat{x}$ is perpendicular to the plane.
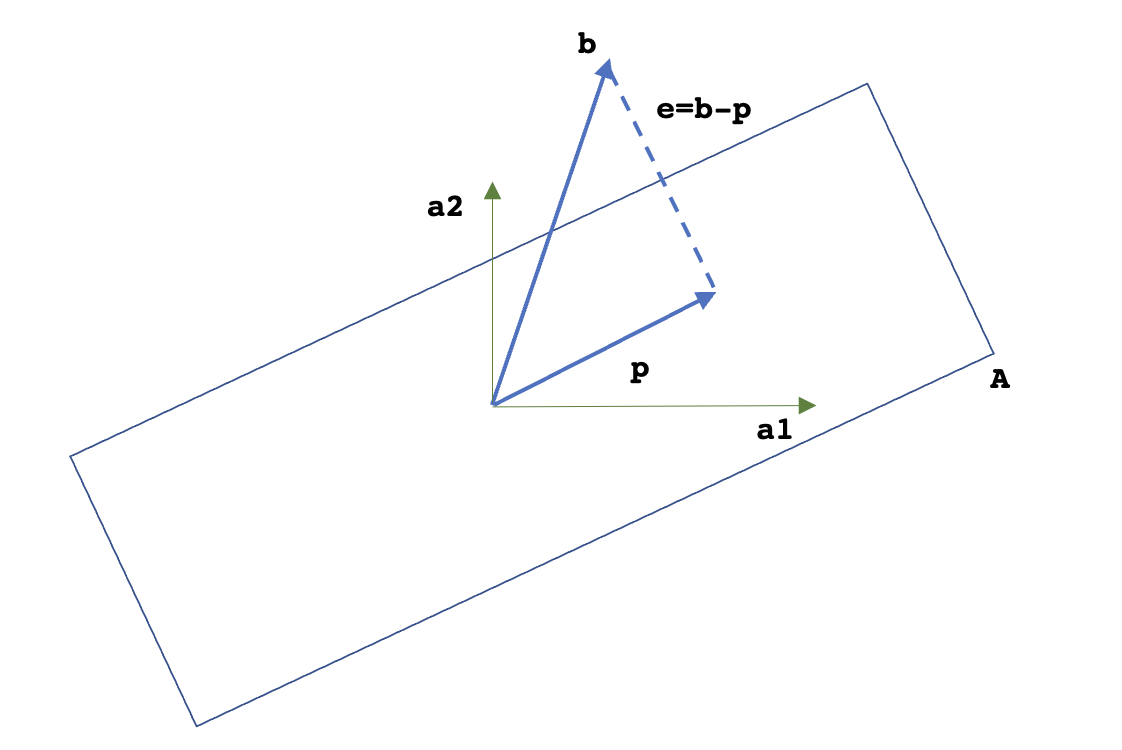
Or, we can say that the error vector $e$ is perpendicular to both the basis vectors $a_1$ and $a_2$, i.e. $a_1^T(b-A\hat{x}) = 0$ and $a_2^T(b-A\hat{x}) = 0$. In the matrix form, $\begin{bmatrix}a_1^T \\ a_2^T\end{bmatrix}(b - A\hat{x}) = \begin{bmatrix}0 \\ 0\end{bmatrix}$ or $A^T(b-A\hat{x}) = 0$.
This equation tells us that the error vector $e = b-A\hat{x}$ is in the null space of $A^T$. We know that the null space of $A^T$ is perpendicular to the column space of $A$. This means that the above derived equation is sound. The above equation can be rewriten as: $A^TA\hat{x} = A^Tb$. Hence,
$$\begin{align} \hat{x} = (A^TA)^{-1}A^Tb \end{align}$$
$$\begin{align} p = A\hat{x} = A(A^TA)^{-1}A^Tb \end{align}$$
$$\begin{align} P = A(A^TA)^{-1}A^T \end{align}$$
The projection matrix $P$ holds the properties: $P^T=P$ and $P^2=P$.