24.1 Positive Definite Matrices
These are the complete tests for a $2 \times 2$ matrix $A = \begin{bmatrix} a & b \\ b & c \end{bmatrix}$ for being Positive Definite:
- Both the eigenvalues should be positive: $\lambda_1 > 0;\lambda_2 > 0$
- All the sub-determinants should be positive: $a > 0; ac - b^2 > 0$
- Pivots should be positive: $a>0;\frac{ac-b^2}{a} > 0$
- $x^TAx > 0;\forall x$
The matrix for which any of these conditions holds with equality instead are called as positive semi-definite matrices. For example, the matrix $A = \begin{bmatrix} 2 & 6 \\ 6 & 18 \end{bmatrix}$ is a positive-semidifinite matrix. Let us run the $x^TAx > 0$ test on this matrix. Let $x = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$, then
$$\begin{align} x^TAx = \begin{bmatrix} x_1 & x_2 \end{bmatrix}\begin{bmatrix} 2 & 6 \\ 6 & 18 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = 2x_1^2 + 12x_1x_2 + 18x_2^2 \end{align}$$
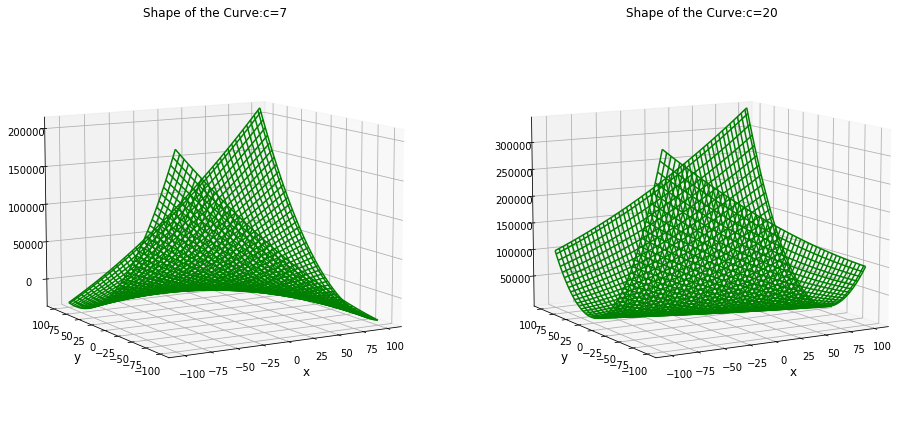
The matrix $A$ is not positive definite as $x^TAx \not>0;\forall x$. If we take $A = \begin{bmatrix} 2 & 6 \\ 6 & 7 \end{bmatrix}$, this matrix is definitely not positive definite. The expression $x^TAx = 2x^2 + 12xy + 7y^2$ where $x = \begin{bmatrix} x \\ y \end{bmatrix}$. For $A = \begin{bmatrix} 2 & 6 \\ 6 & 20 \end{bmatrix}$, the matrix is positive definite as $x^TAx = 2x^2 + 12xy + 20y^2 > 0$ for all values. The plot of $x^TAx$ for two matrices is shown in below figure.
from mpl_toolkits import mplot3d
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return 2*(x ** 2) + 12*x*y + 7*(y ** 2)
x = np.linspace(-100, 100, 100)
y = np.linspace(-100, 100, 100)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
fig = plt.figure(figsize=(16, 30))
ax = fig.add_subplot(1, 2, 1, projection='3d')
ax.plot_wireframe(X, Y, Z, color ='green')
ax.view_init(10, -120)
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
ax.set_title('Shape of the Curve:c=7');
def f(x, y):
return (2*(x ** 2)) + (12*x*y) + (20*(y ** 2))
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
ax = fig.add_subplot(1, 2, 2, projection='3d')
ax.plot_wireframe(X, Y, Z, color ='green')
ax.view_init(10, -120)
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
ax.set_title('Shape of the Curve:c=20');
Another way to find whether $x^TAx$ is always positive or not is by completing the square. For example, $x^TAx = 2x^2 + 12xy + 20y^2 = 2(x+3y)^2 + 2y^2$, and hence $x^TAx$ is always positive. One of the important thing to note that the numbers which come in completing the square come from the row elimination steps with the pivot $2$ outside and the row-multiplier $3$ inside.
$$\begin{align} A = \begin{bmatrix} 2 & 6 \\ 6 & 20 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 3 & 1 \end{bmatrix}\begin{bmatrix} 2 & 6 \\ 0 & 2 \end{bmatrix}=LU \end{align}$$
This can seen be one of the reasons for the pivots being positive for a positive definite matrix as positive pivots will give us positive completed square.
Let us take a $3 \times 3$ matrix $A = \begin{bmatrix} 2 & -1 & 0 \\ -1 & 2 & -1 \\ 0 & -1 & 2 \end{bmatrix}$. Is this matrix positive definite? The values of sub-determinants of this matrix are: $2,3,4$ and hence it is positive definite. We can find the pivots using the fact that product of pivots give us the determinants. Hence first pivot is $2$, second pivot is $\frac{3}{2}$ and the third pivot is $\frac{4}{2 \times \frac{3}{2}} = \frac{4}{3}$. Pivots are also positive and hence the matrix is positive definite.